
在自然界中一些具有复杂几何性质但局部符合一定数学规律的图形,其图案可以在数学上得到推导和重现,这种符合奇妙秩序的图形成为“分形”图形,其在数学、物理、生物学等领域得到广泛应用。
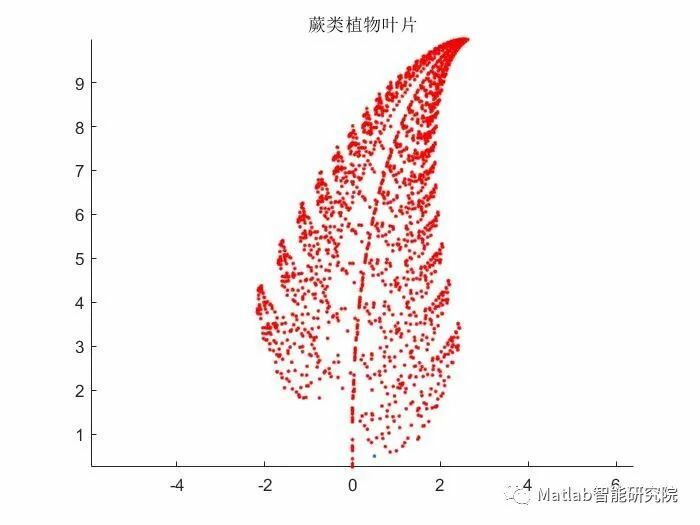
蕨类植物叶片图形绘制
clc;clear;close all;
x = [0.5;0.5]; %定义初值点
figure
hold on
axis([-3,3,0,10]);
plot(x(1),x(2),'.'); %绘制初值点
p = [0.85,0.92,0.99,1.00]; %设置用于判别的随机向量
b1 = [0;1.6];
b2 = [0;1.6];
b3 = [0;0.44];
%仿射变换矩阵
A1 = [0.85,0.04;-0.04,0.85];
A2 = [0.20,-0.26;0.23,0.22];
A3 = [-0.15,0.28;0.26,0.24];
A4 = [0,0;0,0.16];
for i = 1:2000
r = rand; %产生随机数
if r < p(1)
x = A1*x + b1;
elseif r< p(2)
x = A2*x + b2;
elseif r < p(3)
x = A3*x + b3;
else
x = A4*x;
end
plot(x(1),x(2),'r.'); %采用红色绘制叶片颜色
end
axis equal;
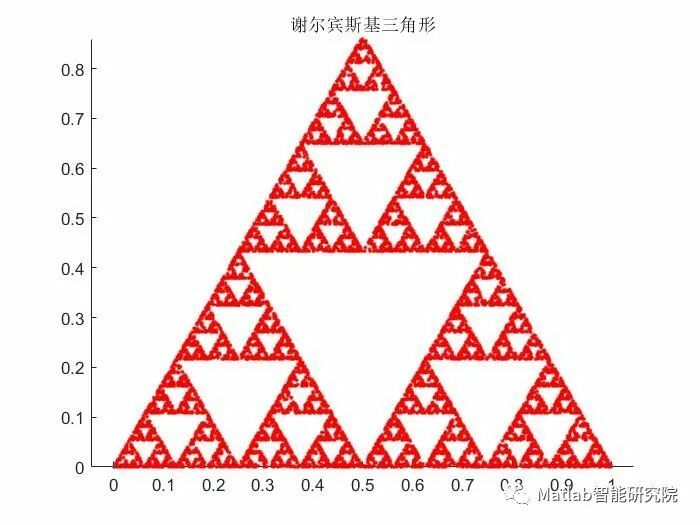
谢尔宾斯基三角形图形绘制
clc;clear;close all;
x = [0;0]; %定义初值点
figure
hold on
title('谢尔宾斯基三角形');
plot(x(1),x(2),'.'); %绘制初值点
A = [0.5,0;0,0.5]; %仿射变换矩阵
b1 = [0,0]';
b2 = [0.5,0]';
b3 = [0.25,sqrt(3)/4]';
for i = 1:10000
r = rand; %产生随机数
if r > 1/3*2
x = A*x+b1;
elseif r > 1/3
x = A*x+b2;
else
x = A*x+b3;
end
plot(x(1),x(2),'r.'); %绘制图形
end
axis equal
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。

评论(0)