
% 定义并绘制一个椭圆,a为椭圆的长轴,b为椭圆的短轴
clc;clear;close all
a=5; % 椭圆的长轴
b=2; % 椭圆的短轴
f=@(x,y) x.^2/a^2+y.^2/b^2-1; % 椭圆的隐函数方程
fimplicit(f,'LineWidth',2); % 使用隐函数绘图命令绘制椭圆
set(gcf,'units','normalized','position',[0.2 0.2 0.6 0.6]); % 设置 figure 窗口的位置和尺寸
grid on
axis equal
axis([-(a+0.5),(a+0.5),-(b+0.5),(b+0.5)]) % 设置坐标轴刻度范围
pause(2)
hold on
% 绘制椭圆的包络矩形
rectangle('Position',[-a,-b,2*a,2*b],'EdgeColor','r','LineWidth',2) % 绘制椭圆的包络矩形
A=4*a*b; % 计算包络矩形的面积
pause(2)
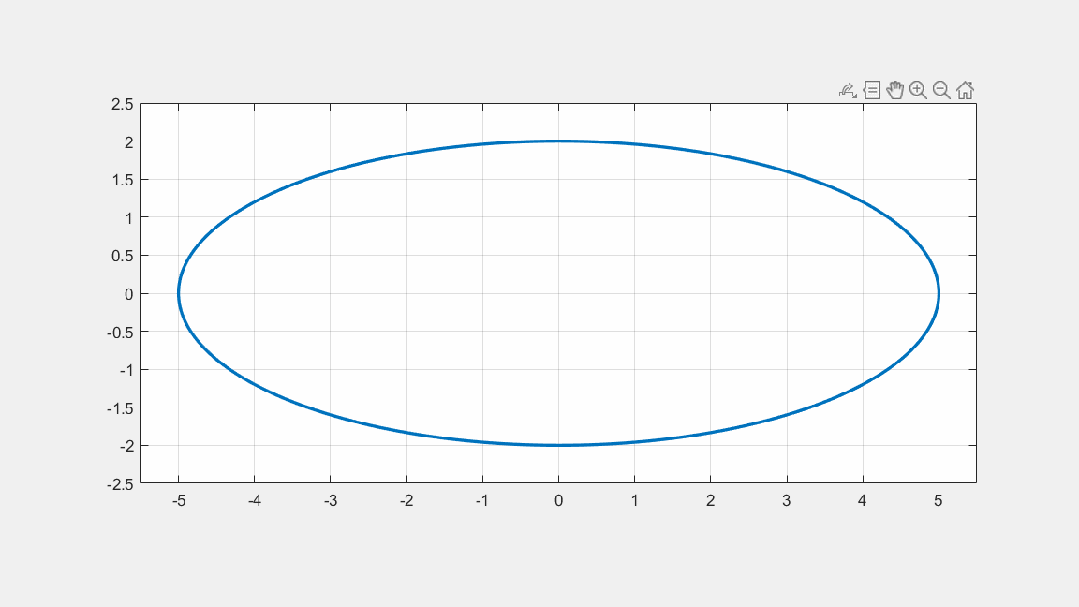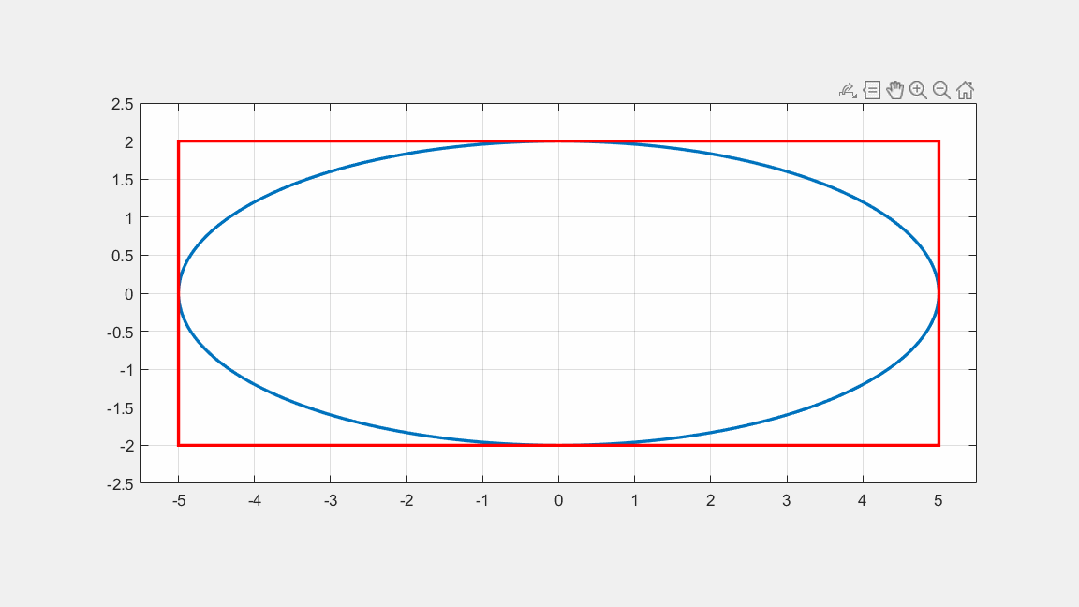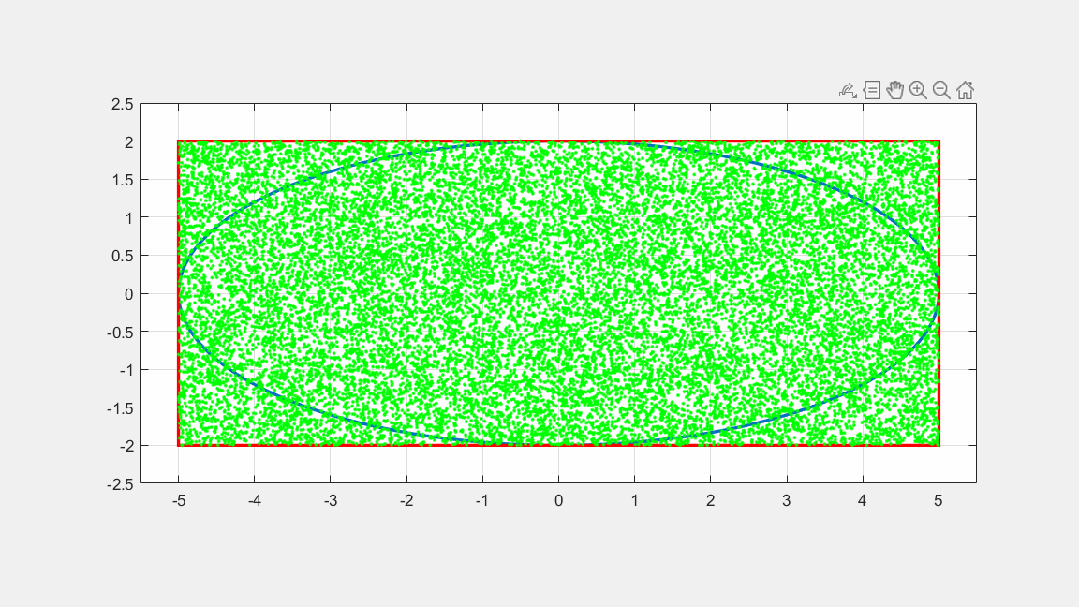
% 往矩形区域里, 投放 N 个均匀分布的随机点,N的值越大求得的椭圆的近似面积精度越高 N=20000; xk=-a+(a+a)*rand(1,N); % 随机点的 x 坐标 yk=-b+(b+b)*rand(1,N); % 随机点的 y 坐标 scatter(xk,yk,'g.'); % 统计落在椭圆里面的, 随机点的个数, 近似求椭圆面积 r=xk.^2/a^2+yk.^2/b^2; % 随机点是否落在椭圆里的判据 m=find(r<=1); % 找到落在椭圆里面的随机点 n=length(m); % 统计落在椭圆里面的, 随机点的个数 S=(n/N)*A % 蒙特卡洛法, 近似求椭圆面积
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。

评论(0)