【Matlab】微积分导数及高阶导数符号运算

导数是微积分中的一个重要概念，在数学中，我们经常利用导数求切线、极值、拐点、渐近线等问题。根据导数的定义，即根据目标函数，当自变量的增量趋于零时，因变量的增量与自变量的增量的比值的极限值为目标函数在该点处的导数值，Matlab内置了diff接口，用于对目标函数进行求导，其调用方式主要分为以下四种：

• diff(S)：采用默认符号变量对函数进行求导，使用findsym函数寻找符号自变量。
• diff(S,’v’)或diff(S,sym(‘v’))：符号表达式S对自变量v进行求导。
• diff(S,n)：类似diff(S)用法，但计算n次导数。
• diff(S,’v’,n)：对符号变量S对自变量v进行求解n次导数。

在实际使用中，我们经常会对特定的因变量进行求导，因此经常使用的以下两种调用方式：

• diff(S,x)：表达式S对x变量求导。
• diff(S,x,n)：表达式S对x求解n阶导数。

实例

一阶导数

clc;clear;close all;
%一阶导数
syms x;
f1=(1+sin(x))/(1-cos(x)) ;
%计算导数
df1=diff(f1,x)
%把窗口拆分为两个子窗口绘图
subplot(1,2,1);ezplot(f1);grid on;
subplot(1,2,2);ezplot(df1);grid on;

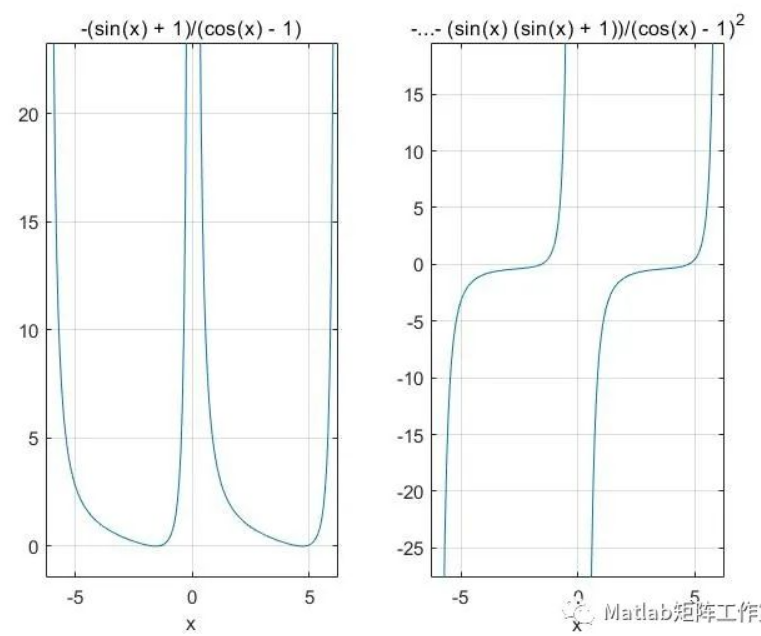
一阶矩阵导数

clc;clear;close all;
%一阶矩阵导数
syms x;
y1=asin(x);
y2=acos(x);
y3=atan(x);
y4=acot(x);
%建立符号矩阵
y=[y1 y2;y3 y4];
%计算符号矩阵导数
dy=diff(y)
figure(2)
%把窗口拆分四小格，画出矩阵函数图像
subplot(2,2,1);ezplot(y1);grid on;
subplot(2,2,2);ezplot(y2);grid on;
subplot(2,2,3);ezplot(y3);grid on;
subplot(2,2,4);ezplot(y4);grid on;
%新建窗口，画出矩阵函数导数图像
figure(3)
subplot(2,2,1);ezplot(dy(1));grid on;
subplot(2,2,2);ezplot(dy(3));grid on;
subplot(2,2,3);ezplot(dy(2));grid on;
subplot(2,2,4);ezplot(dy(4));grid on;

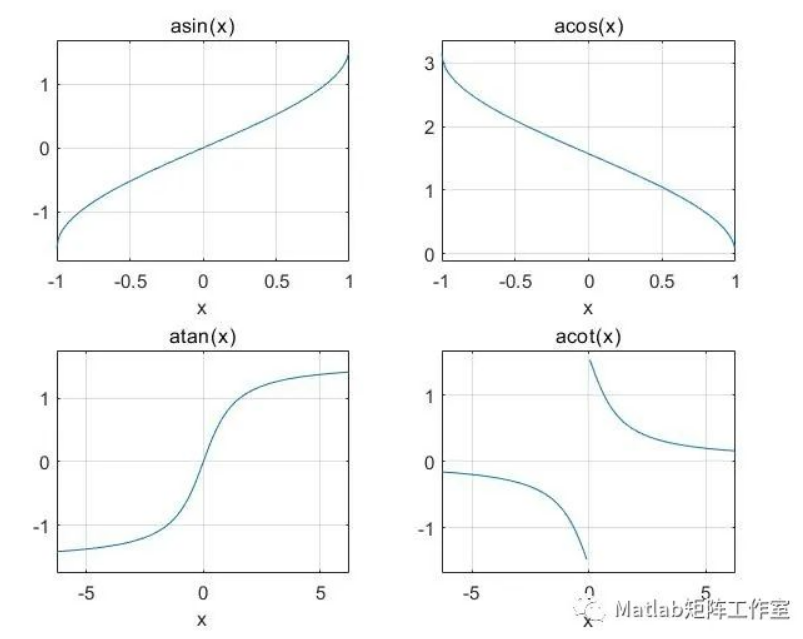
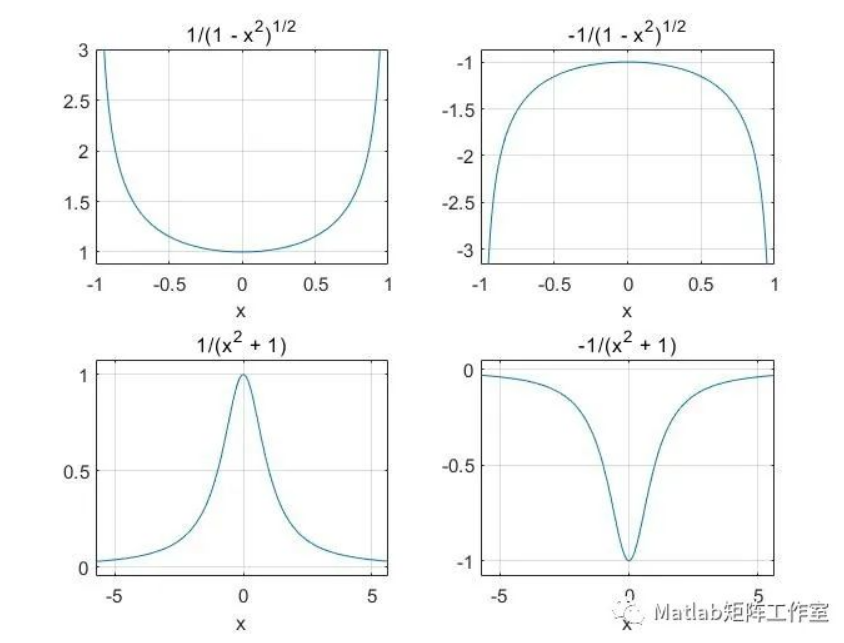
高阶导数

clc;clear;close all;
%高阶导数
syms x;
z=x^2*cos(x);
dz8=diff(z,x,8)
figure(4)
subplot(1,2,1);ezplot(z);grid on;
%在第二子窗口画出高阶导数图像
subplot(1,2,2);ezplot(dz8);grid on;