
% 绘制两个三维曲面
clc;clear;close all
x=-2:0.2:2; % 定义 x 的范围
y=-2:0.2:2; % 定义 y 的范围
[xx,yy]=meshgrid(x,y); % xy 平面的网格化处理
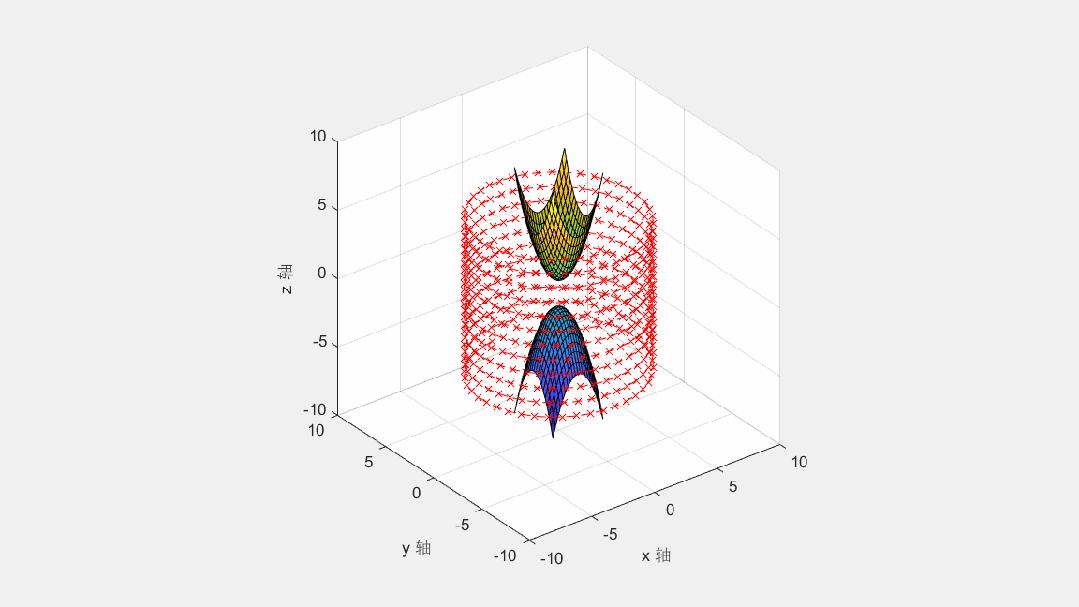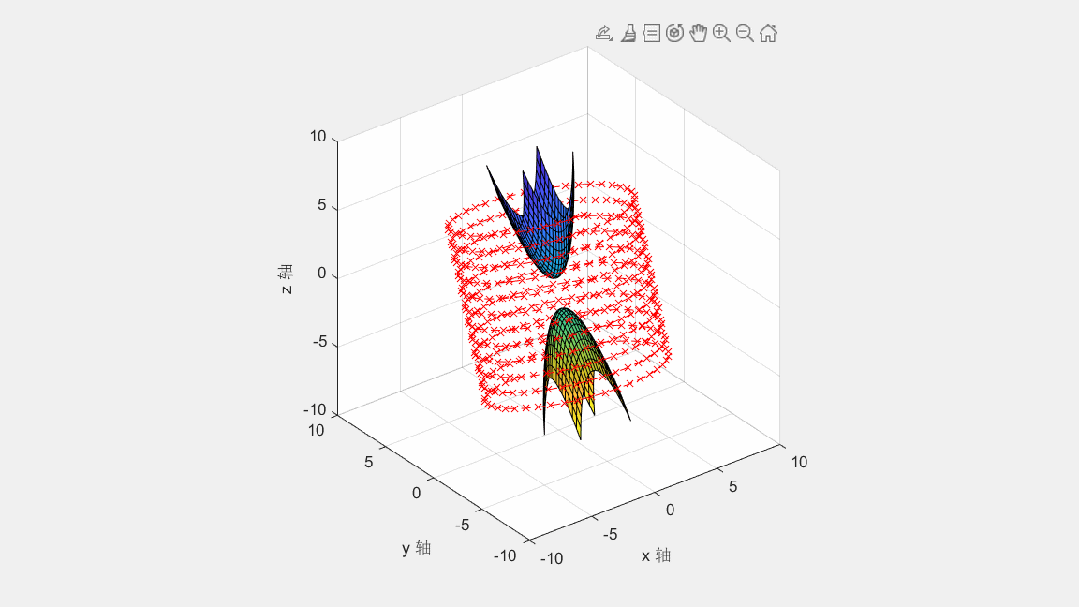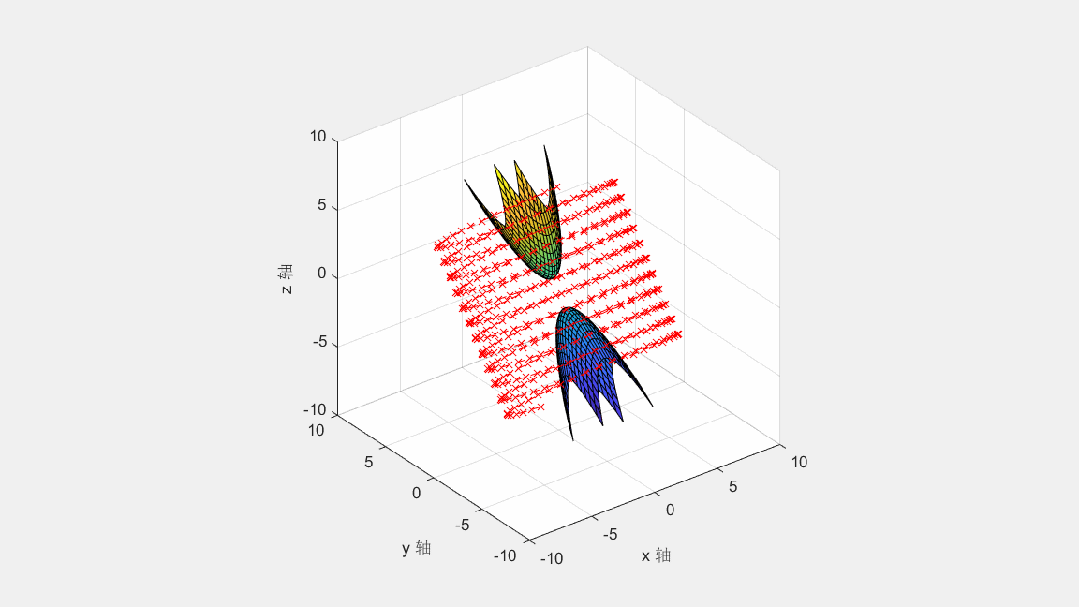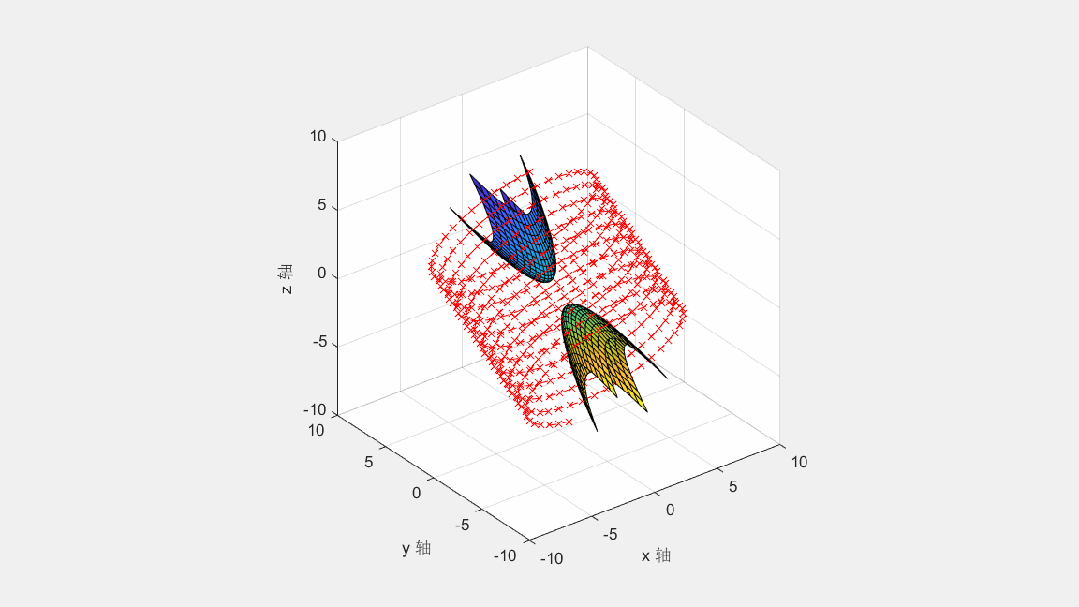
zz1=xx.^2+yy.^2+1; % 计算第一个曲面的 z 坐标
zz2=-xx.^2-yy.^2-1; % 计算第二个曲面的 z 坐标
figure
set(gcf,'units','normalized','position',[0.2 0.2 0.6 0.6]); % 设置 figure 窗口的位置和尺寸
h1=surf(xx,yy,zz1);
hold on
h2=surf(xx,yy,zz2);
% 绘制一个三维螺旋线
t=-12:0.05:12;
xk=6*cos(3*t);
yk=6*sin(3*t);
zk=0.5*t;
h3=plot3(xk,yk,zk,'--xr');
% 设置坐标系的属性
axis equal
set(gca,'XLim',[-10 10])
set(gca,'YLim',[-10 10])
set(gca,'ZLim',[-10 10])
xlabel('x 轴')
ylabel('y 轴')
zlabel('z 轴')
% 将三维曲面和三维螺旋线, 添加到同一个几何变换组里
t=hgtransform; % 创建一个几何变换组 t
set(h1,'Parent',t) % 将曲面句柄 h1 的父对象, 设置为 t (将 h1 添加到几何变换组 t 里)
set(h2,'Parent',t) % 将曲面句柄 h2 的父对象, 设置为 t (将 h2 添加到几何变换组 t 里)
set(h3,'Parent',t) % 将三维螺旋线句柄 h3 的父对象, 设置为 t (将 h3 添加到几何变换组 t 里)
% 对整个几何变换组, 实施绕 x 轴旋转的操作
for rx_angle=0:0.1:2.7*pi
Rx=makehgtform('xrotate',rx_angle); % 求出绕 x 轴旋转的变换矩阵
set(t,'Matrix',Rx) % 使用变换矩阵, 对几何变换组 t 实施整体绕 x 轴的旋转操作
pause(0.05);
end
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。

评论(0)